前言：

　　关于Sparse coding目标函数的优化会涉及到矩阵求数问题，因为里面有好多矩阵范数的导数，加上自己对矩阵运算不熟悉，推导前面博文中关于拓扑（非拓扑的要简单很多）Sparse coding代价函数对特征变量s导数的公式时，在草稿纸上推导了大半天也没有正确结果。该公式表达式为：

　　  

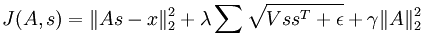
　　后面继续看UFLDL教程，发现这篇文章中已经给出了我想要的答案，作者是应用BP神经网络中求网络代价函数导数的思想，将上述代价函数演变成一个多层的神经网络，然后利用每层网络中节点的误差值来反向推导出每一层网络节点的导数。Andrew Ng真值得人佩服，给出的教程切中了我们的要害。

　　在看怎样使用BP思想计算矩阵范数的导数时，先看下针对这种问题求解的BP算法形式（和以前经典的BP算法稍有不同，比如说最后一层网络的误差值计算方法，暂时还没弄明白这样更改的理由）：

1. 对网络（由代价函数转换成的网络）中输出层中节点的误差值，采用下面公式计算：

 　　

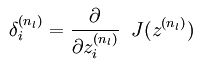
　　2.  从网络的倒数第2层一直到第2层，依次计算网络每层的误差值：

 　　

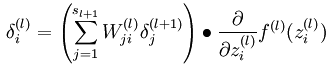
　　3.  计算网络中l层的网络参数的偏导（如果是第0层网络，则表示是求代价函数对输入数据作为参数的偏导）：

 　　

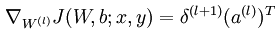
　　比如在上篇博文中，就使用过将矩阵范数转换成矩阵的迹形式，然后利用迹的求导公式得出结果，那时候是求sparse coding中非拓扑网络代价函数对权值矩阵A的偏导数，现在用BP思想来求对特征矩阵s的导数，代价函数为：

 　　

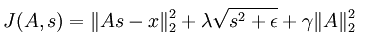
　　将表达式中s当做网络的输入，依次将公式中各变量和转换关系变成下面的网络结构：

 　　

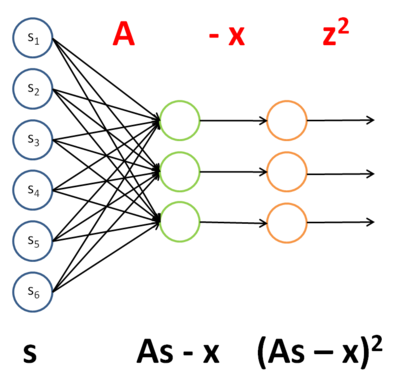
　　列出每一层网络的权值，activation函数及其偏导数，误差值，每一层网络的输入，如下所示：

 　　

　　求最后一层网络的误差值时按照前面BP算法的方法此处是：最后一层网络的输出值之和J对最后一层某个节点输入值的偏导，这里的J为：

                                                                                         

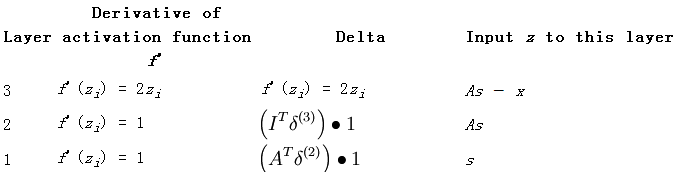
　　因为此时J对Zi求导是只对其中关于Zi的那一项有效，所以它的偏导数为2*Zi。

　　最终代价函数对输入X（这里是s）的偏导按照公式可以直接写出如下：

 　　

 

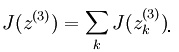
　　下面继续来看那个我花了解决一天时间也没推倒出来的偏导数，即在拓扑sparse coding代价函数中关于特征矩阵s的偏导公式。也就是本文一开始给出的公式。

　　用同样的方法将其转换成对应的网络结构如下所示：

 　　

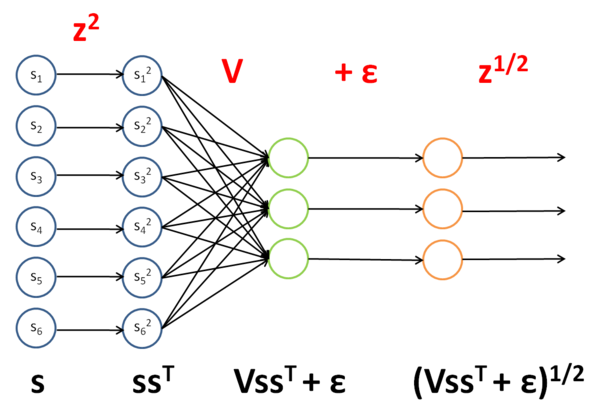
　　也同样的，列出它对应网络的参数：

 　　

　　 

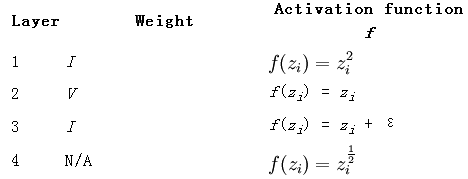
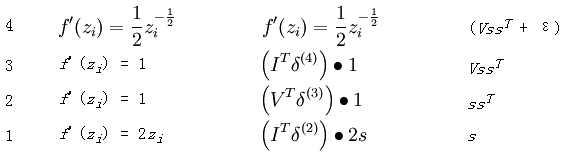
　　其中的输出函数J如下：

　　

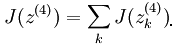
　　最终那个神奇的答案为：

 　　 

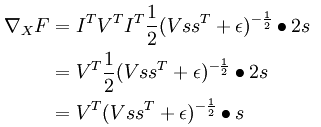
　　看来这种方法得掌握，如果日后自己论文用到什么公式需要推导的话。

 

 

　　参考资料：